0xGame 2024 [Week 2] 报告哈基米

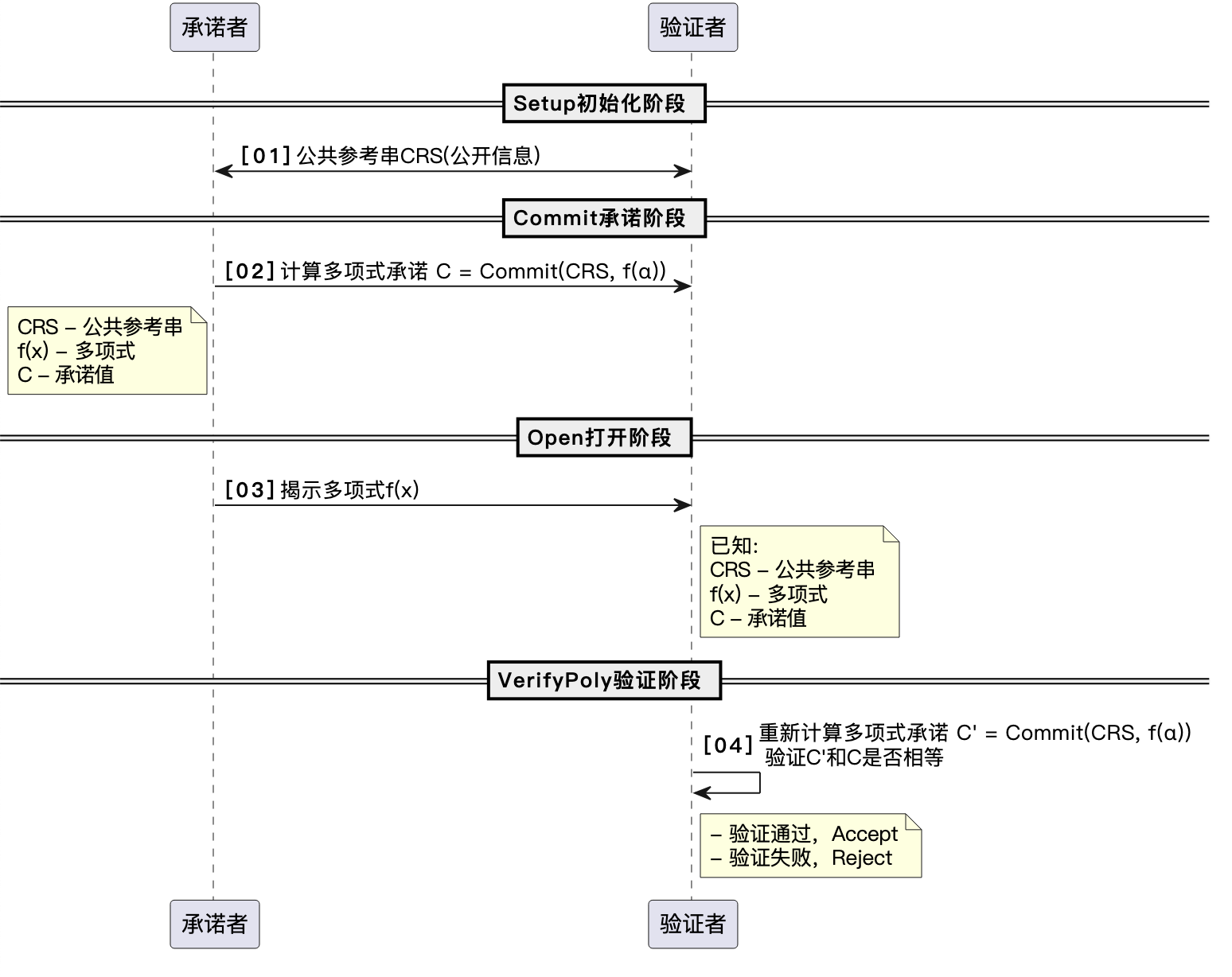
新知识：Tupper（塔珀自指公式）；Arnold Cat（猫映射）

下载文件是一个png图片，010打开查看

发现是倒着的pk

转一下保存为zip文件，打开后是一个txt文件

有两个地方有提示，一个是十六进制里面的Maybe You Need To Kown Arnold Cat？还有一个是txt里面的Is This Tupper？

去搜一下Tupper是什么

代码急转弯——Tupper（塔珀自指公式）-CSDN博客

其代码运行出来的图片就是公式本身，在txt文件中第一句是倒序，所以我们也将下面的k值进行逆序，下面是在网上找的大佬的代码，应该是有三个算法在里面，我们就用Tupper一个就好了，把k值丢进去跑一下得到图片

########################################################################
#
#
#                    Tupper’s Self-Referential Formula
#                             Tupper.py
#
#                                MAIN
#
#                 Copyright (C) 2015 Ulrik Hoerlyk Hjort
#
#  Tupper’s Self-Referential Formula is free software;  you can  redistribute it
#  and/or modify it under terms of the  GNU General Public License
#  as published  by the Free Software  Foundation;  either version 2,
#  or (at your option) any later version.
#  Tupper’s Self-Referential Formula is distributed in the hope that it will be
#  useful, but WITHOUT ANY WARRANTY;  without even the  implied warranty
#  of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
#  See the GNU General Public License for  more details.
#  You should have  received  a copy of the GNU General
#  Public License  distributed with Yolk.  If not, write  to  the  Free
#  Software Foundation,  51  Franklin  Street,  Fifth  Floor, Boston,
#  MA 02110 - 1301, USA.
########################################################################

from PIL import Image


# Tupper
k1=9489414856877039590479997730148554425666925984049232945604842888420596111937489062065081199094002132087091572191187170308560128611026043144427876131133135794969867759108490917632153891963456295991713868378392769549376070709924497237322046334486274987407067993824142187115870972520417207510521083293280152434558803258138899515603807505064799735152359900010019631133734298562293682916239050320580346316026460860919542540955914826806059123630945216006606268974979135253968165822806241305783300650874506602000048154282039485531804337171305656252


# Pacman
# k2=144520248970897582847942537337194567481277782215150702479718813968549088735682987348888251320905766438178883231976923440016667764749242125128995265907053708020473915320841631792025549005418004768657201699730466383394901601374319715520996181145249781945019068359500510657804325640801197867556863142280259694206254096081665642417367403946384170774537427319606443899923010379398938675025786929455234476319291860957618345432248004921728033349419816206749854472038193939738513848960476759782673313437697051994580681869819330446336774047268864


# Euler
# k3=2352035939949658122140829649197960929306974813625028263292934781954073595495544614140648457342461564887325223455620804204796011434955111022376601635853210476633318991990462192687999109308209472315419713652238185967518731354596984676698288025582563654632501009155760415054499960

# Assign k1,k2, k3 to k to get desired image
k = k1
width = 106
height = 17
scale = 5

fname = "foo"
image  = Image.new("RGB", (width, height),(255, 255, 255))

for x in range (width):
    for y in range (height):
        if ((k+y)//17//2**(17*int(x)+int(y)%17))%2 > 0.5:
            # Image need to be flipped vertically - therefore y = height-y-1
            image.putpixel((x, height-y-1), (0,0,0))


#scale up image
image = image.resize((width*scale,height*scale))
image.save(fname+".png")

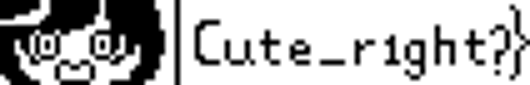
看大括号的位置，这应该是flag的后半段

找Arnold Cat是个什么东西

在数学中，阿诺德猫映射是一种从环面到自身的混沌映射，以弗拉基米尔·阿诺德的名字命名，他于 20 世纪 60 年代使用猫的图像展示了它的效果，因此得名。该图的一个特点是图像在变换过程中看似随机化，但经过若干步骤后又恢复到原始状态。猫的原始图像在变换的第一次迭代中被剪切然后重新包裹。经过几次迭代后，生成的图像看起来相当随机或无序，但经过进一步的迭代后，图像似乎有了进一步的秩序——猫的幽灵般的图像、以重复结构排列的多个较小的副本，甚至是原始图像的颠倒副本——并最终恢复到原始图像。

发现最初的图片看起来非常无序，应该是经过了猫映射（https://github.com/zhanxw/cat github代码）（https://www.jasondavies.com/catmap/ 在线网站）

不知道咋回事网站和代码运行后都得不到原图，看起来还是很无序

卡死在这了

最后看了大佬的wp，太强了，脚本一运行直接出来了，放一下脚本

from PIL import Image

img = Image.open('mijiha.png')
if img.mode == "P":
    img = img.convert("RGB")
assert img.size[0] == img.size[1]
dim = width, height = img.size

st = 1
a = 35
b = 7
for _ in range(st):
    with Image.new(img.mode, dim) as canvas:
        for nx in range(img.size[0]):
            for ny in range(img.size[0]):
                y = (ny - nx * a) % width
                x = (nx - y * b) % height
                canvas.putpixel((y, x), img.getpixel((ny, nx)))
canvas.show()
canvas.save('result.png')

得到图片

得到flag前半段，题解

总结：遇到了两个从来没有见过的算法，算是长了见识