主页

微信公众号：密码应用技术实战
博客园首页：https://www.cnblogs.com/informatics/
GIT地址：https://github.com/warm3snow

简介

多项式承诺是一种实用性比较强的密码学承诺方案，允许一个方（承诺者）向另一个方（验证者）承诺一个多项式的值，而不泄露多项式的具体形式。在零知识证明、可验证密码共享等领域有广泛应用，常见的多项式承诺有Kate多项式承诺、FRI多项式承诺，IPA多项式承诺等。本文将重点介绍Kate多项式承诺的构造和应用。

在阅读下文之前，了解基础的密码学承诺原理和应用是非常有必要的，读者可以参考以下几篇文章：
《密码学承诺之原理和应用 – 概览》
《密码学承诺zhi原理和应用 – Sigma承诺》
《密码学承诺之原理和应用 – Pedersen承诺》

前言

多项式

在详细介绍Kate多项式承诺之前，我们先来简单介绍一下多项式的基本概念。多项式一般表示为：

[f(x) = a_0 + a_1x + a_2x^2 + cdots + a_dx^d = sum_{i=0}^{d}a_ix^i
]

上述多项式中，(a_0, a_1, a_2, …, a_d)是多项式系数，(x)是多项式的变量，(d)是多项式的次数(或多项式的度)。多项式的次数是指多项式中最高次幂的指数，例如上述多项式的次数为(t),因此上述(f(x))我们也称作d次多项式。多项式系数(a_0, a_1, a_2, …, a_d)是多项式的重要组成部分，它们决定了多项式的形状和性质，也是需要保护的重要信息。

多项式的值是指将变量x代入多项式后的结果，例如(f(beta))表示将(x=beta)代入多项式中，计算出的结果。

多项式的根是指多项式的值为0的点，即(f(x) = 0)的点。

多项式有两个重要的性质：

一元n次多项式最多有n个根，假设根为(beta_1, beta_2, …, beta_d)，则多项式可以表示为：(f(x) = (x-beta_1)(x-beta_2)…(x-beta_d))
商多项式，多项式减去在某一个点的多项式值(如点：<(a, f(a))>), 可以被另一个多项式整除，这个多项式称为商多项式。商多项式表示为(h(x) = frac{f(x)-f(a)}{x-a})

注：在零知识证明中，通常会将要证明的问题转化为多项式表达，并通过多项式与商多项式的等式关系来进行证明。

双线性映射

在多项式承诺验证中，会用到双线性映射的概念。双线性映射（Bilinear Map）是数学中一种重要的映射，尤其在密码学和数论中有广泛的应用。它是一种特殊的函数，具有以下性质：

定义

设(G)是一个乘法循环群, (g)是一个生成元, (G_T)是另一个群。一个映射(e: G times G rightarrow G_T)被称为双线性映射，如果满足以下条件：

双线性：对于任意的(a, b in Z_p)和(g, h in G)，有(e(g^a, h^b) = e(g, h)^{ab})
非退化性：对于任意的(g in G)，(e(g, g) neq 1)
可计算性：对于任意的(g, h in G)，(e(g, h))可以在多项式时间内计算

重要性质：

可交换性：对于任意的(g, h in G)，(e(g, h) = e(h, g))
分配性：对于任意的(g, h1, h2 in G)，(e(g, h1 cdot h2) = e(g, h1) cdot e(g, h2))
(e(g, g)为G_T)的一个生成元

多项式承诺

多项式承诺主要流程如下：

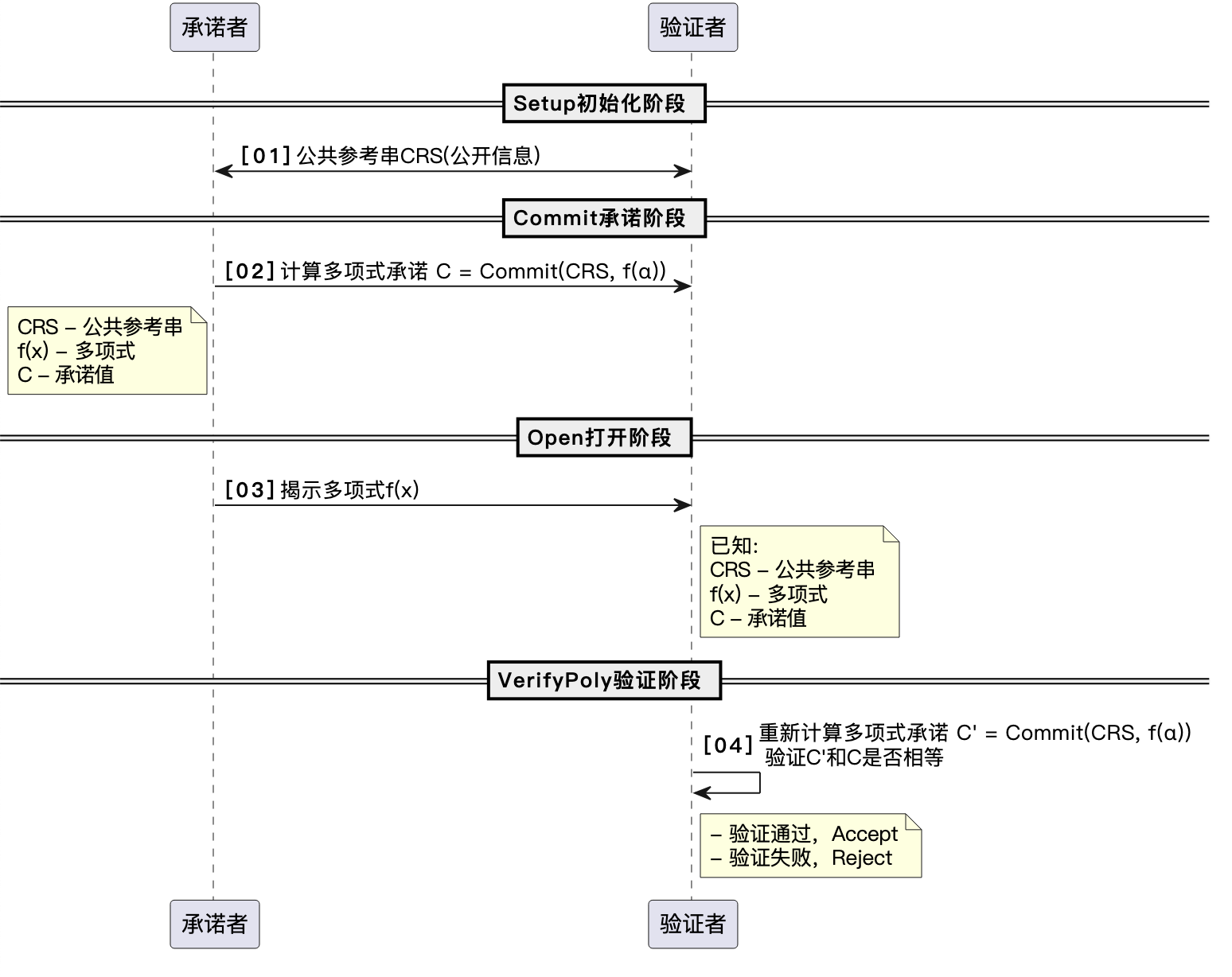
[00] Setup初始化阶段：承诺者和验证者共享公共参考串CRS
- CRS：common reference string，是一个公开的字符串，一般通过可信的第三方生成，用于多项式承诺的构造
[01] Commit承诺阶段：承诺者计算多项式承诺(C = Commit(CRS, f(α)))，并发送(C)给验证者。
- C的计算依赖于多项式(f(x))和公共参考串CRS
- 注在多项式承诺中，多项式的度需要满足(d leq t)，其中(t)是公共参考串中的最高幂次
[02] Open打开阶段：承诺者揭示多项式(f(x))
- f(x)是多项式的具体形式，承诺者直接揭示多项式(f(x))，如多项式参数和系数
[03] VerifyPoly验证阶段：验证者重新计算多项式承诺(C^{‘} = Commit(CRS, f(α)))
- 验证者重新计算多项式承诺(C^{‘})，并验证(C^{‘})和(C)是否相等

以上方式的多项式承诺打开阶段是明文揭示，即承诺者直接揭示多项式(f(x))，验证者重新计算多项式承诺(C^{‘} = Commit(CRS, f(x)))，并验证(C^{‘})和(C)是否相等。
明文揭示的方式简单直接，但存在以下问题：

多项式阶数较高时，明文揭示的方式会导致通信量较大
明文揭示的方式无法保护多项式，必须公开

Kate多项式承诺

为了解决明文揭示多项式承诺存在的问题，Kate多项式承诺基于多项式点打开的方式，实现了多项式的承诺和验证。点打开方式指的是承诺者不直接揭示多项式(f(x))，而是揭示多项式在某个点的值(f(β))，并提供一个witness证明，验证者通过双线性映射验证多项式在β点的值是否正确。通过点打开的方式，Kate多项式承诺解决了明文揭示的问题，同时保护了多项式的隐私。

Kate多项式承诺的构造一般有两种方案，两种方案在安全性上有所不同：

计算隐藏的Kate多项式承诺：承诺的值在计算上是隐藏的，意味着对于任何多项式时间的攻击者，无法有效区分两个不同的承诺。换句话说，攻击者在计算上无法从承诺中推断出承诺的内容。
无条件隐藏的Kate多项式承诺：承诺的值在计算上是无条件隐藏的，意味着对于任何攻击者，无法从承诺中推断出承诺的内容。

定义上比较抽象，简单来说就是无条件隐藏通过引入随机性，使得承诺的值在计算上无法被推断出来，而计算隐藏仅使用离散对数困难性假设，使得承诺的值在计算上无法被推断出来。

计算隐藏的Kate多项式承诺

计算隐藏的Kate多项式承诺的构造如下:

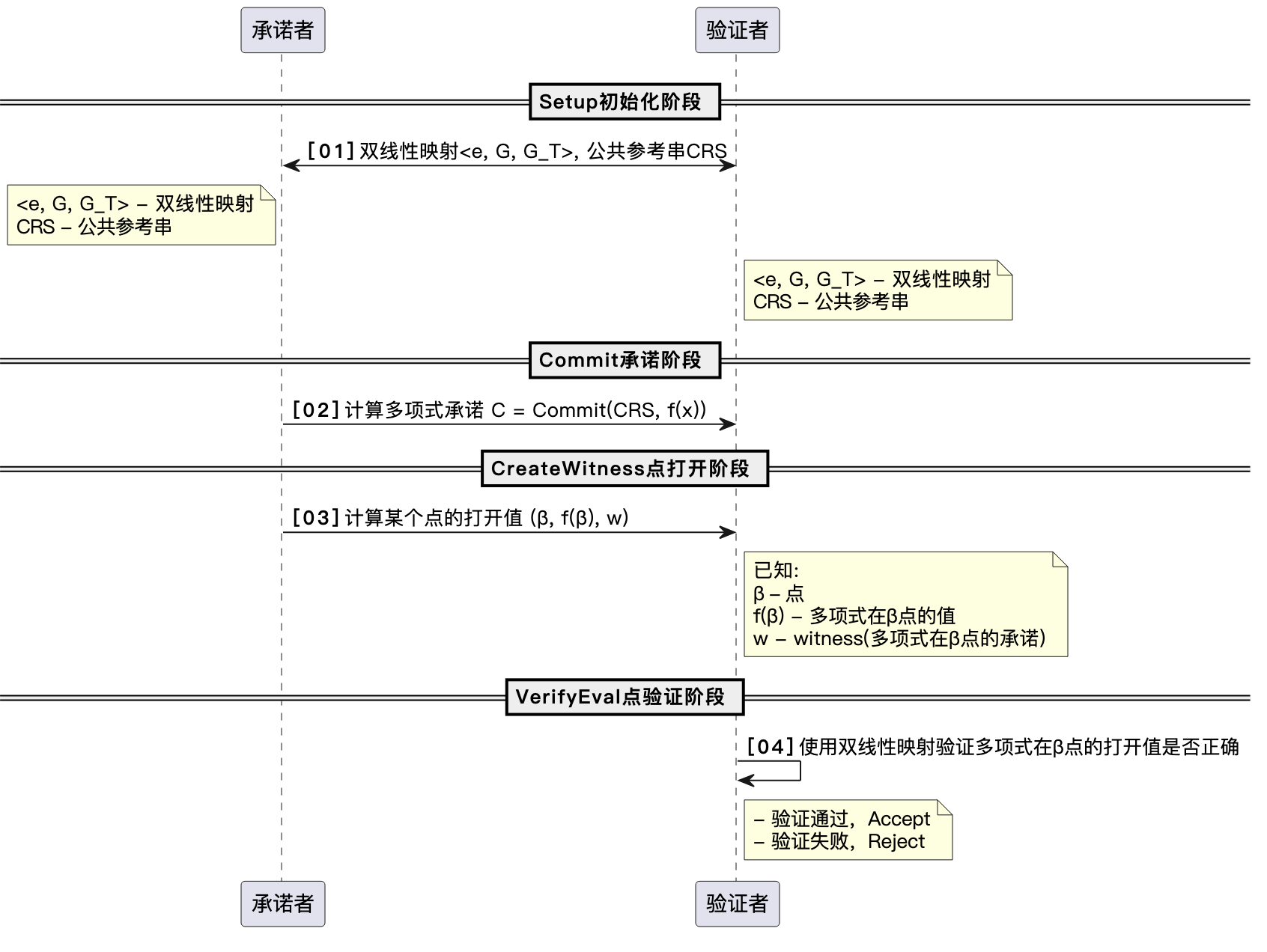
[00] Setup初始化阶段

Kate多项式承诺需要初始化阶段，主要是生成和公开CRS，以及双线性映射(e: G times G rightarrow G_T)。在Kate多项式承诺中CRS如下：

[CRS = (G, g^α, g^{α^2}, …, g^{α^t})
]

其中，(G)代表乘法群，(g)是(G)的一个生成元，(α)是一个随机数，(t)是最高幂次。注：在零知识证明中，(α)是一个私密的值，不会公开，需要被安全销毁（通常被称为有毒废料）。

注：在Kate论文中，CRS被叫做PK，即公钥。

[01] Commit承诺阶段

承诺者计算多项式的承诺值(C = Commit(CRS, f(x)))，并发送(C)给验证者。多项式的承诺值计算方式如下：

[C = g^{f(α)} = g^{sum_{i=0}^{d}{a_iα^i}} = prod_{i=0}^{d}g^{a_iα^i} = prod_{i=0}^{d}{(g^{α^i})^{a_i}}
]

(a_i)是多项式的系数, 承诺者已知
CRS是公共参考串，CRS中包含了(g^{α^i})的值，因此承诺者可以在不知道(α)的情况下计算(C)

[02] CreateWitness点打开阶段

承诺者计算多项式在某个点的值(f(β))，并提供一个witness证明(w)，其中(w)是多项式在β点的承诺，计算方式如下：

首先计算商多项式

[φ(x) = frac{f(x) – f(β)}{x – β} = sum_{i=0}^{d-1}b_ix^i
]

计算(f(x))在β点的值

[f(β) = sum_{i=0}^{d}a_iβ^i
]

计算商多项式在α点的承诺值

[w = Commit(CRS, φ(x))

= g^{φ(α)} = g^{sum_{i=0}^{d-1}{b_iα^i}}

= prod_{i=0}^{d-1}g^{b_iα^i} = prod_{i=0}^{d-1}{(g^{α^i})^{b_i}}
]

承诺者将((β, f(β), w))发送给验证者。

[03] VerifyEval点验证阶段

验证者使用双线性映射验证多项式在β点的打开值是否正确，验证方式如下：

[e(C, g) stackrel{?}{=} e(w, g^{α}/g^{β}) cdot e(g, g)^{f(β)}
]

正确性验证：

[e(w, g^{α}/g^{β}) cdot e(g, g)^{f(β)}

= e(g^{φ(α)}, g^{α-β}) cdot e(g, g)^{f(β)}

= e(g,g)^{φ(α) cdot (α-β)+f(β)}
]

根据商多项式的定义，有：(f(α) – f(β) = φ(α) cdot (α-β))，因此：

[e(w, g^{α}/g^{β}) cdot e(g, g)^{f(β)}

= e(g,g)^{f(α)-f(β)+f(β)}

= e(g,g)^{f(α)}

= e(g^{f(α)}, g)

= e(C, g)
]

因此，(e(C, g) = e(w, g^{α}/g^{β}) cdot e(g, g)^{f(β)})，验证通过。

无条件隐藏的Kate多项式承诺

无条件隐藏的Kate多项式承诺构造与计算隐藏的Kate多项式承诺流程类似，区别在于：

初始化阶段的CRS不同
承诺值的生成和验证方式不同（承诺值生成基于Pedersen承诺）

初始化阶段

CRS的构造如下：

[CRS = (G, g^α, g^{α^2}, …, g^{α^t}, h, h^α, h^{α^2}, …, h^{α^t})
]

其中，(h)是(G)的另一个生成元。

Commit承诺阶段

承诺者计算多项式的承诺值(C = Commit(CRS, f(x)))，计算方式如下：

[C = g^{f(α)} cdot h^{hat{f(α)}}

f(α) = sum_{i=0}^{d}{a_iα^i}

hat{f(α)} = sum_{i=0}^{d}{b_iα^i}

= prod_{i=0}^{d}{(g^{α^i})^{a_i}} cdot prod_{i=0}^{d}{(h^{α^i})^{b_i}}
]

CreateWitness点打开阶段

承诺者计算多项式在某个点的值(f(β))，并提供一个witness证明(w)，计算方式如下：

计算商多项式

[φ(x) = frac{f(x) – f(β)}{x – β}

hat{φ(x)} = frac{hat{f(x)} – hat{f(β)}}{x – β}
]

计算点打开值

[w = Commit(CRS, φ(x)) cdot Commit(CRS, hat{φ(x)})

= g^{φ(α)} cdot h^{hat{φ(α)}}
]

(g^{φ(α)})和(h^{hat{φ(α)}})计算方式基于CRS（方式与上文相同，略），承诺者将((β, f(β), hat{f(β)}, w))发送给验证者。

VerifyEval点验证阶段

验证者使用双线性映射验证多项式在β点的打开值是否正确，验证方式如下：

[e(C, g) stackrel{?}{=} e(w, g^{α}/g^{β}) cdot e(g^{f(β)} cdot h^{hat{f(β)}}, g)
]

正确性验证：

(h)是(G)中的一个群元素，因此不是一般性可设(h = g^lambda)，其中(lambda)是一个随机数。因此：

[e(w, g^{α}/g^{β}) cdot e(g^{f(β)} cdot h^{hat{f(β)}}, g)

= e(g^{φ(α)} cdot h^{hat{φ(α)}}, g^{α-β}) cdot e(g^{f(β)} cdot h^{hat{f(β)}}, g)

= e(g^{φ(α)+lambdahat{φ(α)}}, g^{α-β}) cdot e(g^{f(β)+lambdahat{f(β)}}, g)

= e(g,g)^{φ(α) cdot (α-β)+lambdahat{φ(α)} cdot (α-β) + f(β) + lambdahat{f(β)}}

= e(g,g)^{φ(α) cdot (α-β)+ f(β) + lambda cdot(hat{φ(α)} cdot (α-β) + hat{f(β)})}
]

根据商多项式的定义，有：(f(α) – f(β) = φ(α) cdot (α-β))，(hat{f(α)} – hat{f(β)} = hat{φ(α)} cdot (α-β))，因此：

[e(w, g^{α}/g^{β}) cdot e(g^{f(β)} cdot h^{hat{f(β)}}, g)

= e(g,g)^{φ(α) cdot (α-β)+ f(β) + lambda cdot(hat{φ(α)} cdot (α-β) + hat{f(β)})}

= e(g,g)^{f(α) – f(β)+ f(β) + lambda cdot(hat{f(α)} – hat{f(β)} + hat{f(β)})}

= e(g,g)^{f(α) + lambda cdot hat{f(α)}}

= e(g^{f(α)} cdot g^{lambda cdot hat{f(α)}}, g)

= e(g^{f(α)} cdot h^{hat{f(α)}}, g)

= e(C, g)
]

因此，(e(C, g) = e(w, g^{α}/g^{β}) cdot e(g^{f(β)} cdot h^{hat{f(β)}}, g))，验证通过。

结语

Kate多项式承诺是一种实用性比较强的多项式承诺方案，通过点打开的方式，可以在保护多项式隐私的同时，有效减少通信量。Kate多项式承诺在零知识证明、可验证密码共享等领域有广泛应用。了解Kate多项式承诺的原理和构造，对于学习zk-snarks、zk-starks等零知识证明协议是非常有帮助的。通过本文的介绍，希望读者能够对Kate多项式承诺有一个初步的了解，并为进一步学习零知识证明协议打下基础。

参考文献

千百度

1.本站内容仅供参考，不作为任何法律依据。用户在使用本站内容时，应自行判断其真实性、准确性和完整性，并承担相应风险。

2.本站部分内容来源于互联网，仅用于交流学习研究知识，若侵犯了您的合法权益，请及时邮件或站内私信与本站联系，我们将尽快予以处理。

3.本文采用知识共享署名4.0国际许可协议 [BY-NC-SA] 进行授权

4.根据《计算机软件保护条例》第十七条规定“为了学习和研究软件内含的设计思想和原理，通过安装、显示、传输或者存储软件等方式使用软件的，可以不经软件著作权人许可，不向其支付报酬。”您需知晓本站所有内容资源均来源于网络，仅供用户交流学习与研究使用，版权归属原版权方所有，版权争议与本站无关，用户本人下载后不能用作商业或非法用途，需在24个小时之内从您的电脑中彻底删除上述内容，否则后果均由用户承担责任；如果您访问和下载此文件，表示您同意只将此文件用于参考、学习而非其他用途，否则一切后果请您自行承担，如果您喜欢该程序，请支持正版软件，购买注册，得到更好的正版服务。