LeetCode39. 组合总和
题目叙述:
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
- 输入:candidates = [2,3,6,7], target = 7,
- 所求解集为: [ [7], [2,2,3] ]
示例 2:
- 输入:candidates = [2,3,5], target = 8,
- 所求解集为: [ [2,2,2,2], [2,3,3], [3,5] ]
思路:
- 题目中提到同一个数字可以无限制的被选取,那么我们就想,如果这个数组中有0怎么办?那不是无穷选了?但是我们看到题目中说,所有数字都是正整数,所以我们放心了,我们可以先画出递归搜索树来形象的观察我们这题的操作过程
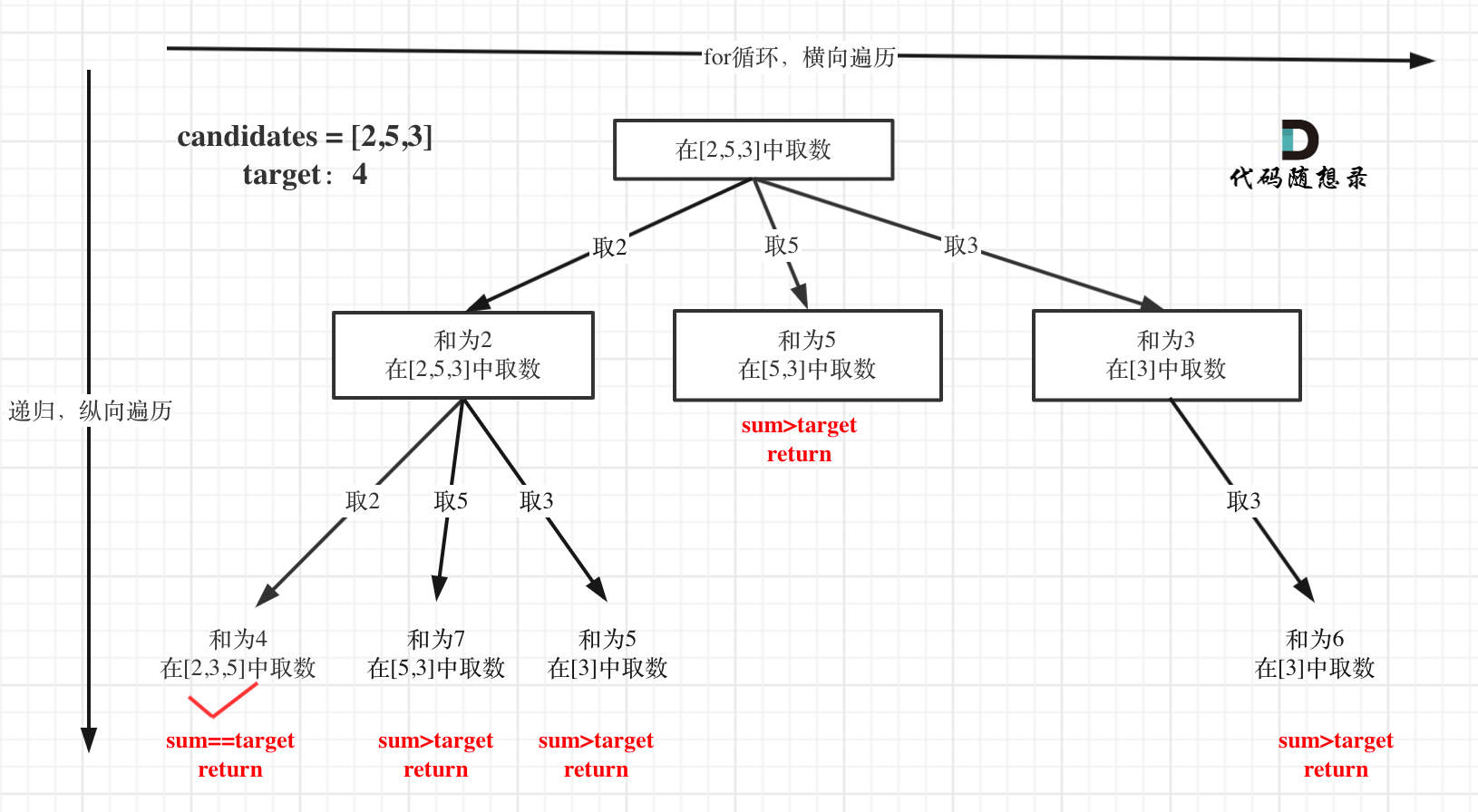
- 注:本图应用了代码随想录的原图,想要了解更加深刻的读者可以去看看原作者的文章:
- [代码随想录 (programmercarl.com)]()
1.回溯函数的参数以及返回值
- 我们需要一个一维数组path存放当前路径上的所有元素,并且需要一个二维数组result存放所有的结果。
- 需要传入一个目标值targetSum,这就是我们的目标和
- 并且我们需要一个sum来记录当前路径所有元素的总和,其实这个也不是必须的,我们可以通过加减targetSum来实现。不过这里我们介绍使用sum的方法,这样更加直观!
2.递归的中止条件
- 注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
//当sum≥targetSum就可以返回了
if(sum>=targetSum){
if(sum==targetSum) result.push_back(path);
return;
}
3. 单层递归的逻辑
-
我们通过for循环来控制横向遍历,通过控制递归函数来实现纵向遍历,不过这里的纵向遍历可就不是i+1了,而是i,这里一定要想清楚,因为这道题说一个元素是可以重复选取的!!!所以说纵向遍历的时候,是可以包括当前遍历的元素的,在代码体现上也就是递归函数的参数startindex==i,而不是i+1。
-
明白了这个之后,我们不难写出代码:
for(int i=startindex;i<candidates.size();i++){
sum+=candidates[i];
path.push_back(candidates[i]);
//这里是i,并不是i+1,因为同一个元素可以重复取
backtracking(candidates,targetSum,sum,i);
sum-=candidates[i];
path.pop_back();
}
- 在这里我们也可以隐藏回溯的过程,代码更简洁,但是初学者不推荐这种写法
for(int i=startindex;i<candidates.size();i++){
path.push_back(candidates[i]);
//将回溯过程隐藏在递归函数当中
backtracking(candidates,targetSum,sum+candidates[i],i);
path.pop_back();
}
代码:
- 通过上面的分析,我们不难得出代码:
class Solution {
public:
vector<int> path;
vector<vector<int> > result;
void backtracking(vector<int> candidates,int targetSum,int sum,int startindex){
if(sum>=targetSum){
if(sum==targetSum) result.push_back(path);
return;
}
for(int i=startindex;i<candidates.size();i++){
//使用sum加减更直观,也可以隐藏到回溯函数当中。
sum+=candidates[i];
path.push_back(candidates[i]);
//这里是i,并不是i+1,因为同一个元素可以重复取
backtracking(candidates,targetSum,sum,i);
sum-=candidates[i];
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
path.clear();result.clear();
if(candidates.size()==0) return result;
backtracking(candidates,target,0,0);
return result;
}
};
1.本站内容仅供参考,不作为任何法律依据。用户在使用本站内容时,应自行判断其真实性、准确性和完整性,并承担相应风险。
2.本站部分内容来源于互联网,仅用于交流学习研究知识,若侵犯了您的合法权益,请及时邮件或站内私信与本站联系,我们将尽快予以处理。
3.本文采用知识共享 署名4.0国际许可协议 [BY-NC-SA] 进行授权
4.根据《计算机软件保护条例》第十七条规定“为了学习和研究软件内含的设计思想和原理,通过安装、显示、传输或者存储软件等方式使用软件的,可以不经软件著作权人许可,不向其支付报酬。”您需知晓本站所有内容资源均来源于网络,仅供用户交流学习与研究使用,版权归属原版权方所有,版权争议与本站无关,用户本人下载后不能用作商业或非法用途,需在24个小时之内从您的电脑中彻底删除上述内容,否则后果均由用户承担责任;如果您访问和下载此文件,表示您同意只将此文件用于参考、学习而非其他用途,否则一切后果请您自行承担,如果您喜欢该程序,请支持正版软件,购买注册,得到更好的正版服务。
5.本站是非经营性个人站点,所有软件信息均来自网络,所有资源仅供学习参考研究目的,并不贩卖软件,不存在任何商业目的及用途












暂无评论内容