最长公共子序列
- 本文讲解的题与leetcode1143.最长公共子序列这题一样,阅读完可以挑战一下。
题目叙述:
给定两个字符串,输出其最长公共子序列,并输出它的长度
输入:
ADABEC和DBDCA
输出:
DBC
3
解释
最长公共子序列是DBC,其长度为3
动态规划思路:
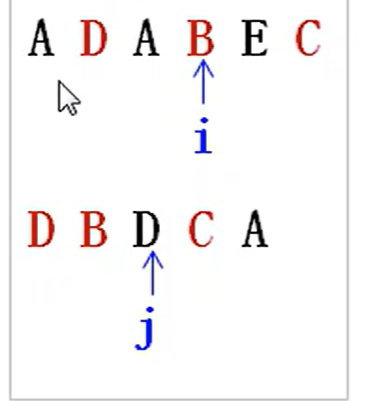
- 我们这题先构建一个模型,我们使用两个指针
i,j,分别用于遍历a字符串,b字符串。如图所示:
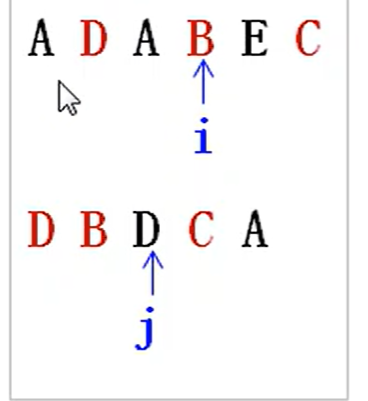
-
然后我们可以设想一个状态变量,也就是一个函数。一个关于两个变量相关的函数,这在代码中体现为二维数组
f。 -
然后
f[i][j]表示什么呢?表示序列a[1,2,3....i]和b[1,2,3....j]的最长公共子序列的长度
状态变量的含义
-
在这里的状态变量为
f[i][j],它的含义是a的前i个字符与b的前j个字符的最长公共子序列的长度 -
现在就要观察
a[i],b[j]是否在当前的最长公共子序列当中。 -
具体情况如下图:

递推公式:
f[i][j]可以分为三种情况讨论,就是:
a[i],b[j]都在最长公共子序列当中,也就是a[i]==b[j]a[i]!=b[j],并且a[i]不在公共子序列当中。a[i]!=b[j],并且b[j]不在公共子序列当中。
- 那我们的递推公式就可与分为两种情况:
f[i][j]=f[i-1][j-1]+1(a[i]==b[j])f[i][j]=max(f[i-1][j],f[i][j-1])(a[i]!=b[j])
- 显而易见,我们的边界条件为:
f[0][j]=0f[i][0]=0
//m是a字符串的长度,n是b字符串的长度
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
//因为我们的f数组是从下标1开始,而字符串是从0开始的下标
if(a[i-1]==b[j-1]) f[i][j]=f[i-1][j-1]+1;
else f[i][j]=max(f[i-1][j],f[i][j-1]);
}
}
遍历顺序
- 经过上面的分析,明显遍历顺序为
i从小到大,j也是从小到大。
初始化
- 初始化边界为0即可
举例打印dp数组
- 如图所示

如何找出对应的最长公共子序列的长度
-
我们使用p数组来记录每一次
f[i][j]的值来源于哪一个方向- 1方向代表左上方
- 2方向代表左方
- 3方向代表上方
-
代码改造如下:
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(a[i-1]==b[j-1]){
f[i][j]=f[i-1][j-1]+1;
//左上方
p[i][j]=1;
}
else if(f[i-1][j]>f[i][j-1]){
f[i][j]=f[i][j-1];
//左边
p[i][j]=2;
}
else{
f[i][j]=f[i-1][j];
//上边
p[i][j]=3;
}
}
}
p[i][j]代表前驱的位置。
算法的执行过程
- 我们要找到最长公共子序列,只需要找到从结尾开始,往前找到
p[i][j]==1,也就是来源于左上方的哪些元素的集合,就是我们的最长公共子序列。(并不是棋盘中所有p[i][j]==1)的元素,而是从右下角出发,往回找到的所有p[i][j]==1的那些元素。 - 例子如下:

-
我们使用
s数组来储存最长公共子序列 -
代码实现:
int i,j,k;
char s[200];
i=m;j=n;k=f[m][n];
while(i>0&&j>0){
//左上方
if(p[i][j]==1){
s[k--]=a[i-1];
i--;j--;
}
//左边
else if(p[i][j]==2) j--;
//上边
else i--;
}
for(int i=1;i<=f[m][n];i++) cout<<s[i];
最终代码实现:
#include <iostream>
#include <cstring>
using namespace std;
char a[200];
char b[200];
int f[205][205];
int p[205][205];
int m, n;
void LCS() {
int i, j;
m = strlen(a);
n = strlen(b);
for (i = 1; i <= m; i++) {
for (j = 1; j <= n; j++) {
if (a[i - 1] == b[j - 1]) {
f[i][j] = f[i - 1][j - 1] + 1;
p[i][j] = 1;
}
else if (f[i - 1][j] > f[i][j - 1]) {
f[i][j] = f[i - 1][j];
p[i][j] = 2;
}
else {
f[i][j] = f[i][j - 1];
p[i][j] = 3;
}
}
}
cout << f[m][n] << endl;
}
//寻找出当初的最长公共子序列。
void getLCS() {
int i = m, j = n, k = f[m][n];
char s[200];
s[k] = '\0';
while (i > 0 && j > 0) {
if (p[i][j] == 1) {
s[--k] = a[i - 1];
i--; j--;
}
else if (p[i][j] == 2) {
i--;
}
else {
j--;
}
}
cout << s << endl;
}
int main() {
cin >> a >> b;
LCS();
getLCS();
return 0;
}
1.本站内容仅供参考,不作为任何法律依据。用户在使用本站内容时,应自行判断其真实性、准确性和完整性,并承担相应风险。
2.本站部分内容来源于互联网,仅用于交流学习研究知识,若侵犯了您的合法权益,请及时邮件或站内私信与本站联系,我们将尽快予以处理。
3.本文采用知识共享 署名4.0国际许可协议 [BY-NC-SA] 进行授权
4.根据《计算机软件保护条例》第十七条规定“为了学习和研究软件内含的设计思想和原理,通过安装、显示、传输或者存储软件等方式使用软件的,可以不经软件著作权人许可,不向其支付报酬。”您需知晓本站所有内容资源均来源于网络,仅供用户交流学习与研究使用,版权归属原版权方所有,版权争议与本站无关,用户本人下载后不能用作商业或非法用途,需在24个小时之内从您的电脑中彻底删除上述内容,否则后果均由用户承担责任;如果您访问和下载此文件,表示您同意只将此文件用于参考、学习而非其他用途,否则一切后果请您自行承担,如果您喜欢该程序,请支持正版软件,购买注册,得到更好的正版服务。
5.本站是非经营性个人站点,所有软件信息均来自网络,所有资源仅供学习参考研究目的,并不贩卖软件,不存在任何商业目的及用途











暂无评论内容