看前建议:
本文以jupyter notebook为编辑器进行示例,建议有一定python基础后再进行学习。
python的安装:https://www.cnblogs.com/scfssq/p/17478132.html
jupyter notebook的安装:https://www.cnblogs.com/kohler21/p/18349764
公众号本文地址:https://mp.weixin.qq.com/s/EocThNWhQlI2zeLcUApsQQ
NumPy简介
公众号:愚生浅末
Numeric Python(简称NumPy)是使用Python进行科学计算的基本包,它是一个Python库,提供了多维数组对象,使用NumPy相较于直接编写Python代码实现,性能更加高效、代码更加简洁。NumPy广泛应用于各类场合,例如在机器学习、数值处理、爬虫等。NumPy主要是围绕Ndarray对象展开,通过NumPy的线性代数库对其进行一系列操作如切片索引、广播、修改数组(形状、维度、元素的增删改)、连接数组等,以及对多维数组的点积等。除了数组,Numpy还有很多函数包括三角函数、统计函数等。
NumPy的重要特点之一就是 n 维数组对象,即 ndarray。
在使用Numpy之前需要线导入Numpy:
import numpy as np
生成数组
- 生成0\1数组
生成0/1数组,利用np.ones(shape, dtype)或np.ones_like(a, shape)、np.zeros(shape, dtype)或np.zeros_like(a, shape)
one_matrix = np.ones([3, 3]) # 生成一个3x3的矩阵,矩阵元素都为1
one_matrix
效果:
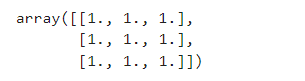
生成一个3×3的矩阵,矩阵元素都为0
zero_matrix = np.zeros_like(one_matrix)
zero_matrix
效果:
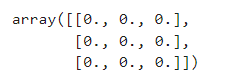
- 从现有数据生成数组,通过np.array(object, dtype)或np.asarray(a, dtype)
arr = np.array([[3, 4],[1, 2]])
print([[3, 4],[1, 2]])
arr
效果:
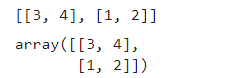
arr1 = np.array(arr)
arr1
效果:

arr2 = np.asarray(arr)
arr2
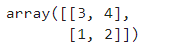
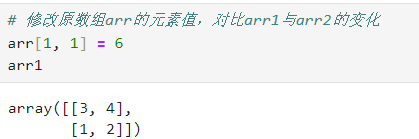
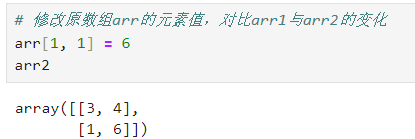
可以发现,arr1和arr2与arr1完全一直,但是采用了不同的函数,实际上这两个复制函数是不同的,对于arr1采用的是np.array(),而arr2采用的是np.asarray()。当修改arr的元素值时候,arr1的元素值不会改变,而arr2的元素值会随着arr的元素值的改变而改变,示例如下:
# 修改原数组arr的元素值,对比arr1与arr2的变化
arr[1, 1] = 6
- 生成固定范围的数组,利用np.arange()
通过np.linspace(start,stop,num=50)、np.arange([start=None],stop=None,[stop=None])、np.logspace(start,stop,num=50)均可以生成指定范围的数字,以np.arange()示例如下:
arr = np.arange(0, 13, 2)
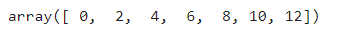
可以发现生成的数组不包含指定的最后一个数字,因为这个区间设定是左闭右开的。
公众号:愚生浅末
4. 生成随机数组
生成随机数组有多种方法。
rand基本用法
numpy.randon.rand(d0,d1,…dn),产生[0,1)之间均匀分布的随机浮点数,其中d0,d1,…dn标识传入的数组形状。
np.random.rand(2)#产生形状为(2,)的数组,也就是相当于有两个元素的一维数组
np.random.rand(2,4)#产生一个形状为(2,4)的数组,数组中的每个元素是[0,1)之间均匀分布的随机浮点数

random基本用法
numpy.random.random(size),产生[0,1)之间的随机浮点数,非均匀分布
numpy.random.random_sample、numpy.random.ranf、numpy.random.sample用法与该函数类似
注意:该函数和rand()的区别
(1)random()参数只有一个参数”size”,有3种取值:None,int型整数,int型元组。而在之前的numpy.random.rand()中可以有多个参数。例如,如果要产生一个3*3的随机数组(不考虑服从什么分布),那么在rand()中的写法是:numpy.random.rand(3,3),而在random中的写法是numpy.random.random((3,3)),这里面是个元组,是有小括弧的。
(2)random()产生的随机数的分布为非均匀分布,numpy.random.rand()产生的随机数的分布为均匀分布
#产生一个[0,1)之间的形状为(3,3)的数组
np.random().random((3,3))
#产生[-5,0)之间的形状为(3,3)的随机数组,即5*[0,1)-5
5*np.random.random_sample((3,3))-5
#产生[5,10)之间的形状为(3,3)的随机数组,即10*[0,1)-5[0,1)+5
(10-5)*np.eandom.random_sample((3,3))+5
numpy.random.uniform
np.random.uniform(0.0, 1.0,size=None),从指定范围内产生均匀分布的随机浮点数,如果在seed()中传入的数字相同,那么接下来生成的随机数序列都是相同的,仅作用于最接近的那句随机数产生语句
#默认产生一个[0,1)之间随机浮点数
np.random.uniform()
#默认产生一个[1,5)之间的形状为(2,4)的随机浮点数
np.random.uniform(1,5,size=(2,4))
randn基本用法
np.random.randn(d0,d1,…,dn),产生服从于标准正态分布(均值为0,方差为1)的随机浮点数,使用方法和rand()类似
# 产生形状为(2,)的数组
np.random.rand(2)
# 产生形状为(2,4)的数组
np.random.rand(2,4)
如果要指定正态分布的均值和方差,则可以使用这个公式:
sigma * np.random.randn(...) + mu:2.5 *np.random.randn(2,4) + 3
注意:2.5是标准差(不是方差),3是期望
normal基本用法
numpy.random.normal(loc=0.0, scale=1.0, size=None),产生服从正态分布(均值为loc,标准差为scale)的随机浮点数
#产生均值为1标准差为10形状为(1000,)的数组
np.random.normal(1,10,100)
#产生均值为3标准差为2形状为(2,4)的数组
np.random.normal(3,2,size=(2,4))
randint基本用法
numpy.random.randint(low[,high,size,dtype]),产生[low,high)之间的随机数,如果high不知名,则产生[0,low)之间的随机整数,size可以是int整数,或者int型的元组,标识产生随机数的个数,或者随机数组的形状。dtype标识具体随机数的类型,默认是int,可以指定成int64.
#产生一个[0,10)之间的随机整数
np.random.randint(10)
#产生一个[0,10)之间的随机整数8个,以数组的形式返回
np.random.randint(10,size=8)
#产生一个[5,10)之间的形状为(2,4)的随机整数8个,以数组的形式返回
np.random.randint(5,10,size=(2,4))
choice基本用法
numpy.random.choice(a, size=None, replace=True, p=None),从一维arrary a中按概率p选择size个数组,若a为int,则从np.arrange(a)中选择,若a为array,则直接从a中选择。
numpy.random.choice(5,3)#从np.arrange(a)中等概率选择3个,等价于np.random.randint(0,5,3)
numpy.random.choice(5,3,p=[0.1,0,0.3,0.6,0])#从np.arrange(a)中按概率p选择3个
numpy.random.choice(5,3,p=[0.1,0,0.3,0.6,0]
numpy.random.choice(5,3,replace=False,p=[0.1,0,0.3,0.6,0])
aa_milne_arr = ['pooh','rabbit','piglet','Christopher']
np.random.choice(aa_milne_arr,5,p=[0.5,0.1,0.1,0.3])
numpy.random.shuffle
numpy.random.shuffle(x)按x的第一个维度进行打乱,x只能是array
np.random.shuffle(np.arange(9).reshape((3,3)))#对np.arange(9).reshape((3,3))打乱
numpy.random.permutation
numpy.random.permutation(x),按x的第一个维度进行打乱,若a为int,则对np.arrange(a)打乱,若a为array,则直接对a打乱
np.random.permutation(10)#对np.arange(10)打乱
np.random.permutation(np.arange(9).reshape((3,3)))#对np.arange(9).reshape((3,3))打乱
numpy.random.seed
若果在seed()中传入的数字相同,那么接下来生成的随机数序列都是相同的,仅作用于最接近的那句随机数产生语句
np.random.seed(10)
temp1 = np.random.rand(4)
np.random.seed(10)
temp2=np.random.rand(4)
temp3=np.random.rand(4)
上述temp1和temp2是相同的,temp3是不同的,因为seed仅作用于最接近的那句随机数产生语句。
numpy.linspace
numpy.linspace(start,stop,num=50,endpoint = True,retstep = False,dtype = None,axis = 0),区间均等分
np.linspace(2.0,3.0,num=5) #array([2.,2.25,2.5,2.75,3.])
np.linspace(2.0,3.0,num=5,endpoint=False) #array([2.,2.2,2.4,2.6,2.8])
np.linspace(2.0,3.0,num=5,retstep=True) #(array([2.,2.25,2.5,2.75,3.]),0.25)
zeros(),ones(),empty(),eye(),identity(),diag()
- zeros(),ones(),empty()三者用法一样,np.zeros(3,dtype=int) np.zeros((2,3))
- 使用empty()时需要对生成的每一个数进行重新赋值,否则即为随机数,所以慎重使用
- np.eye(2,3,k=1)he np.identity(3) : np.identity只能创建方形矩阵,np.eye可以创建矩形矩阵,且k值可以调节,为1 的对角线的位置偏离度,0居中,1向上偏离1,2向上偏离2,以此类推,-1向下偏离。值的绝对值过大就偏离出去了,整个矩阵就全是0了。np.diag可以创建对角矩阵。
数组的索引、切片
ndarray的索引、切片与list稍不同,他只有一个'[]’代码如下:
arr = np.array([ [[1, 2, 3],[4, 5, 6]], [[7, 8, 9],[10, 11, 12]] ])
list1 = [ [[1, 2, 3],[4, 5, 6]], [[7, 8, 9],[10, 11, 12]] ]
# 以下两种方法取值相同
a1 = arr[0, :]
b1 = arr[0][:]
print(list1[0][:]) # list只能用两个中括号来取值
print(a1, b1) # [[1, 2, 3][4, 5, 6]]

a2 = arr[0, 0, 0]
print(a2) # 1
可以看到ndarray的切片索引方法就是:对象[x, y, z, …]先行后列,依据对象的纬度输入的参数也不同。对于ndarray来说,以下两种索引方式均可以。
a = [[1, 2, 3],[4, 5, 6]], [[7, 8, 9],[10, 11, 12]]
b = np.array(a)
print(b[0, 1]) # array([4, 5, 6])
print(b[0][1]) # array([4, 5, 6])
而对于二维的list而言,只能使用[][][] []索引
a = [[1, 2, 3],[4, 5, 6]], [[7, 8, 9],[10, 11, 12]]
# b = np.array(a)
# print(a[0, 1]), 该种索引方式会报错
print(a[0][1]) # [4, 5, 6]
形状修改
通过ndarray.T可以实现一个矩阵的转置,代码如下:
arr = np.array([[1, 2],[3, 4]])
arr.T # [[1, 3],[2, 4]]
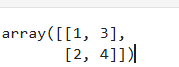
可以通过ndarray.reshapre()将arr变成一个1行4列的数组,reshape()实际上是将原来的数组压平成一维数组,然后再重新排序成目标形状,但不改变原数组。代码如下:
new_arr = arr.reshape([1, 4])
new_arr # [[1, 2, 3, 4]]
也可以通过ndarray.resize()实现改变结构,但是resize()会改变原数组,而不是直接返回一个新数组。代码如下:
arr.resize([1, 4])
arr # [[1, 2, 3, 4]]
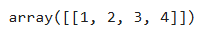
通过np.repeat(a,reps,axis),可以实现对原数组的复制、重构。其中a是目标数组,reps是重复的次数,axis标识沿某个方向复制。若axis=0,则沿第0个维度变化的方向复制,即增加了行数,若axis=None,则原数组会展平成一维数组,代码如下:
arr = np.array([[1, 2], [3, 4]])
flat_arr = np.repeat(arr, 2)
flat_arr # [1, 1, 2, 2, 3, 3, 4, 4]
re_arr = np.repeat(arr, 2, axis = 1)
re_arr # [[1, 1, 2, 2], [3, 3, 4, 4]]
通过np.tile(a, reps),以可以实现对通过复制原数组构建新的数组,其中a是目标数组,reps是重复的次数。相较于np.repeat(),np.tile()的参数更少,但而这实现的功能是类似的,但其复制的规则不同,np.tile()是对整个array进行复制,np.repeat()是对其中的元素进行复制代码如下:
arr = np.array([[1, 2], [3, 4]])
flat_arr = np.tile(arr, 2)
flat_arr # [1, 1, 2, 2, 3, 3, 4, 4]
tile_arr = np.tile(arr, (2, 1))
tile_arr # [[1, 2], [3, 4], [1, 2], [3, 4]]
通过np.concatenate((a, b), axis)可以实现对数组的连接,其中a、b分别标识两个数组;axis表示沿着第几个维度叠加,例如,axis=0时,即沿第0个维度变化的方向相加,代码如下:
a = [[1, 2], [3, 4]]
b = [[10, 11], [12, 13]]
res1 = np.concatenate((a, b), axis = 0)
res1 # [[1, 2], [3, 4], [10, 11], [12, 13]]
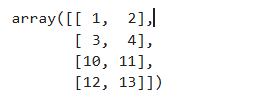
res2 = np.concatenate((a, b), axis = 1)
res2 # [[1, 2, 10, 11], [3, 4, 12, 13]]
此外,np.vstack((a, b))的作用与np.concatenate((a, b), axis = 0)相似,np.hstack((a, b))的作用与np.concatenate((a, b), axis = 1)相似,代码如下:
v_res = np.vstack((a, b))
v_res # [[1, 2], [3, 4], [10, 11], [12, 13]]
h_res = np.hstack((a, b))
h_res # [[1, 2, 10, 11], [3, 4, 12, 13]
类型修改
首先生成一个数组,代码如下:
# 生成数组
arr = np.array([[1, 2], [3, 4]])
可以通过ndarray.astype(str)将这个数组中的每个元素都变成string类型,该方法不改变原数组,而是返回一个新数组,代码如下:
arr1 = arr.astype(str)
arr1 # [['1' '2'], ['3' '4']]
数组的通用函数
通过np.unique()可以实现对一个现有数组,除去其中重复的元素,返回一个没有重复元素的一维数组,且这个方法不会改变原数组,代码如下:
arr = np.array([[1, 1, 2, 3],[1, 22, 34, 5]])
unique = np.unique(arr)
unique # [1, 2, 3, 5, 22, 34]
如果按某个维度去重,则使用axis指定去重维度即可,代码如下:
a = [[1, 2, 3],[4, 5, 6]], [[1, 2, 3],[4, 5, 6]]
b = np.array(a)
c = np.unique(b, axis=0)
print(c) # array([[[1, 2, 3], [4, 5, 6]]])
通过np.intersect1d()和np.union1d(),可以分别实现求两个矩阵的交集和并集。代码如下:
a = [1, 2, 3, 4]
b = [3, 4, 5, 6]
print(np.intersect1d(a, b)) # [3, 4]
print(np.union1d(a, b)) # [1, 2, 3, 4, 5, 6]
Numpy中还有一些常用的一元函数、二元函数,在原数组进行操作,直接修改原数组的元素。np.abs(),可以实现计算浮点数、整数或复数的绝对值.
a = [-1, 2, -3, 4]
print(np.abs(a)) # [1, 2, 3, 4]
np.sqrt(),可以实现计算元素的平方根,相当于Python中的“ ** ”的反函数
b = [3, 4, 5, 6]
print(np.sqrt(b)) # [1.73205081, 2, 2.23606798, 2.44948974]
print(2**2)
np.square()计算各元素的平方,np.exp()可以计算各元素的e指数,np.power(arr, t)可以计算数组中各元素t次方
# np.square()计算各元素的平方,np.exp()可以计算各元素的e指数,np.power(arr, t)可以计算数组中各元素t次方
a = [-1, 2, -3, 4]
print(np.square(a)) # [1, 4, 9, 16]
print(np.exp(a)) # [3.67879441e-01, 7.38905610e+00, 4.97870684e-02, 5.45981500e+01]
print(np.power(a, 3)) # [ -1, 8, -27, 64]
np.isnan()用于判断数组中哪些元素是空值
c = [1, np.nan, 3, 5]
print(np.isnan(c)) # [False, True, False, False]
np.sum(np.isnan(c))
np.where()可以对数组进行筛选,有两种用法:
1、np.where(condition, x, y):x, y是两个数组,condition指选择条件,若满足条件则输出x,否则,输出y;
2、np.where(condition):condition是一个条件,输出数组中满足条件的下标。
a = [[1, 2], [3, 0]]
b = [[7, 8], [9, 1]]
c = [1, 2, 3, 4]
print(np.where([[True, False], [False, False]], a, b)) # [[1, 2], [9, 0]]
np.where(np.array(c)>2)
c = np.array(a)
np.where(c > 1)
输出结果:
(array([0, 1], dtype=int64), array([1, 0], dtype=int64))
Numpy也实现了三角函数的计算,np.sin(),np.cos(),np.tan()
a = [-1, 2, -3, 4]
print(np.sin(a)) # [-0.84147098, 0.90929743, -0.14112001, -0.7568025 ]
print(np.cos(a)) # [ 0.54030231, -0.41614684, -0.9899925, -0.65364362]
print(np.tan(a)) # [-1.55740772, -2.18503986, 0.14254654, 1.15782128]
线性代数
NumPy的中的np.linalg模块实现了许多矩阵的基本操作,如:求对角线元素,求对角线元素的和(求迹)、矩阵乘积、求解矩阵行列式等。
首先生成两个数组,代码如下:
# 生成两个数组
a = [1, 2, 3]
b = [[1, 3, 9], [2, 7, 0], [4, 3, 2]]
通过np.diag(matrix),matirx为一个矩阵,当matrix为二维数组时,以一维数组的形式返回方阵的对角线;当matrix为一维数组时,则返回非对角线元素均为0的方阵。
print(np.diag(a)) # [[1, 0, 0], [0, 2, 0], [0, 0, 3]]

print(np.diag(b)) # [1, 7, 2]
通过np.trace(),可以计算矩阵对角线元素的迹
print(np.trace(b)) # 10
通过np.dot()可以实现矩阵乘积
print(np.dot(b, a)) # [34, 16, 16]
通过np.det()可以计算矩阵的行列式
np.linalg.det(b) # -196.00000000000009
np.linalg.eig()可以计算方阵的特征值、特征向量
eig = np.linalg.eig(b)
array([-4.40641364, 9.92452468, 4.48188896])
# 特征值
eig[0] # [-4.40641364, 9.92452468, 4.48188896]

# 特征向量
eig[1] # [[0.86881121, -0.6982852, 0.69750503], [-0.15233731, -0.47753756, -0.55399068], [-0.47112676, -0.53325009, 0.4545119]]
np.linalg.inv()可以计算矩阵的逆
np.linalg.inv(b) # [[-0.07142857, -0.10714286, 0.32142857], [0.02040816, 0.17346939, -0.09183673], [0.1122449, -0.04591837, -0.00510204]]

np.linalg.solve(A,b)可以求解线性方程组Ax=b,A为一个方阵
np.linalg.solve(b,a) # [0.67857143, 0.09183673, 0.00510204]
np.linalg.svd(a, full_matrices = 1, compute_uv = 1)可以用于矩阵的奇异值分解,返回该矩阵的左奇异值(u)、奇异值(s)、右奇异值(v)
svd = np.linalg.svd(b)
svd

统计分析
1) 通过np.sum(a, axis)计算数组a沿指定轴的和;
2) np.mean(a,axis)计算数组a沿指定轴的平均值;
3) min(axis)和a.max(axis)用于获取数组a,沿指定轴的最小值和最大值;
4) np.std(a,axis)计算数组a沿指定轴的标准差;
5) np.var(a,axis)计算数组a沿指定轴的方差;
6) np.argmin(a,axis)和np.argmax(a,axis)分别用于获取数组a,沿指定轴的最小值和最大值的索引。
注:axis=None时,会返回所有元素的和;axis=0时,会沿着第0个维度(也就是列)的变化方向进行计算,即按列求和;axis=1时,则为按行求和,以此类推。
a = np.array([[1, 2, 3], [4, 5, 6]])
# 通过np.sum(a, axis)计算数组a沿指定轴的和
print(np.sum(a)) # 21
print(np.sum(a, axis=0)) # [5, 7, 9]
# np.mean(a,axis)计算数组a沿指定轴的平均值
print(np.mean(a, axis=1)) # [2, 5]
# min(axis)和a.max(axis)用于获取数组a,沿指定轴的最小值和最大值
print(a.min(axis=0)) # [1, 2, 3]
# np.std(a,axis)计算数组a沿指定轴的标准差
print(np.std(a, axis=1)) # [0.81649658, 0.81649658]
# np.argmin(a,axis)和np.argmax(a,axis)分别用于获取数组a,沿指定轴的最小值和最大值的索引
print(np.argmax(a, axis=1)) # [2, 2]
公众号:愚生浅末
欢迎关注公众号:愚生浅末
公众号本文地址:https://mp.weixin.qq.com/s/EocThNWhQlI2zeLcUApsQQ
1.本站内容仅供参考,不作为任何法律依据。用户在使用本站内容时,应自行判断其真实性、准确性和完整性,并承担相应风险。
2.本站部分内容来源于互联网,仅用于交流学习研究知识,若侵犯了您的合法权益,请及时邮件或站内私信与本站联系,我们将尽快予以处理。
3.本文采用知识共享 署名4.0国际许可协议 [BY-NC-SA] 进行授权
4.根据《计算机软件保护条例》第十七条规定“为了学习和研究软件内含的设计思想和原理,通过安装、显示、传输或者存储软件等方式使用软件的,可以不经软件著作权人许可,不向其支付报酬。”您需知晓本站所有内容资源均来源于网络,仅供用户交流学习与研究使用,版权归属原版权方所有,版权争议与本站无关,用户本人下载后不能用作商业或非法用途,需在24个小时之内从您的电脑中彻底删除上述内容,否则后果均由用户承担责任;如果您访问和下载此文件,表示您同意只将此文件用于参考、学习而非其他用途,否则一切后果请您自行承担,如果您喜欢该程序,请支持正版软件,购买注册,得到更好的正版服务。
5.本站是非经营性个人站点,所有软件信息均来自网络,所有资源仅供学习参考研究目的,并不贩卖软件,不存在任何商业目的及用途










暂无评论内容